How does Compression Work?
There are two main types of compression methods - lossless compression and lossy compression. Huffman Tree compression is a method by which the original data can be reconstructed perfectly from the compressed data, and hence it belongs to the lossless compression family.
How does Huffman Tree Compression Work?
Huffman Tree achieves compression through the use of
variable length code. For the sake of illustration, let's say we want
to compress a text file containing the text:
"Madam, I'm Adam."
In a regular text file, each character would take up 1 byte (8 bits). Since there are 16 characters (counting white spaces and punctuations), it would normally take up 16 bytes. However, why do we need to assign 1 byte to each character in the first place?
There are 256 possible characters under the ASCII code, and this leads us to use 8 bits to represent each character. In any text file, however, we do not necessarily have to use all 256 characters. Furthermore, some characters are used more often, for example, in an English text, the character 'e' probably appears more often than the character 'z'. To acheive compression, we can use a shorter bit string to represent a more frequently occuring characters, and a longer bit string to represent a less frequently occuring characters. We do not have to represent all 256 characters (and hence we can probably use much less than 8 bits per character), unless they all appear in the document we are trying to compress.
Back to my example, we can, for example use the one bit to represent 'a'. Just by doing this, we can use less than 14 bytes to represent the sentence.
This leads to a problem, however. If we use the following codes (assigned from 0 to 7, with '0' being the shortest string and '111' being the longest string):
M:11
a: 0
d: 10
m: 01
,: 100
I: 101
': 110
A : 111
"Madam,I'mAdam."
Encode: 110101000110010111011110001
Decode: 'IaaaMaa.....
You can see the problem. There would be more than one way to interpret the code if we split the code at different places (into codewords). It would be terribly inefficient if we use some special characters to separate two codewords - because we are trying to use less than 1 byte to represent a character, and a special character would take up 1 byte already!
Hence, we need to use only prefix codes. If we make sure that for every codeword, there is no codeword whose prefix is also a codeword, then we can uniquely separate a code into codewords. For example, if 0, 110 and 11 are codewords, then we say prefix code is not used, because 11 is the prefix of 110. When we try to decode '1100', we can separate it into 110|0, or 11|0|0. This problem is not present in fix-length code (e.g. ASCII) because we know that each code is exactly 8 bits long.
How do we then, find the prefix codes/codewords for each character, while keeping them as short as possible? We build a binary tree:
1. Initialization: Put all nodes in an OPEN list, keep it sorted at all times (e.g., ABCDE).
2. Repeat until the OPEN list has
only one node left:
(a) From OPEN pick two nodes having the lowest
frequencies/probabilities, create a parent node of them.
(b) Assign the sum of the children's frequencies/probabilities to the
parent node and insert it into OPEN.
(c) Assign code 0, 1 to the two branches of the tree, and delete the
children from OPEN.
A tree is built using the steps illustrated above. When a tree is built, we assign codewords to each character as in the following example (which is different from the example we have been using):
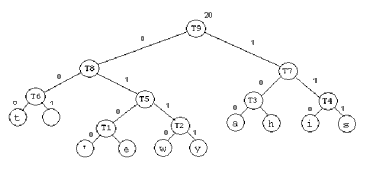
t: 000
': 0100
e: 0101
w: 0110
y: 0111
a: 100
h: 101
i: 110
s: 111
We note that the codes generated are prefix codes, because the characters only appear at the leaf level of the tree.
When we use the codewords generated to encode a document, we achieve compression because the codewords are generally shorter than 8 bits long.